Đoạn thẳng là một khái niệm cơ bản trong hình học, và việc tính toán độ dài của đoạn thẳng là một kỹ năng quan trọng không chỉ trong toán học mà còn trong nhiều lĩnh vực khác như vật lý, kỹ thuật và công nghệ. Bài viết này sẽ giới thiệu chi tiết về công thức tính độ dài đoạn thẳng, cách áp dụng công thức này trong các bài toán thực tế, và những ứng dụng của nó trong cuộc sống hàng ngày.
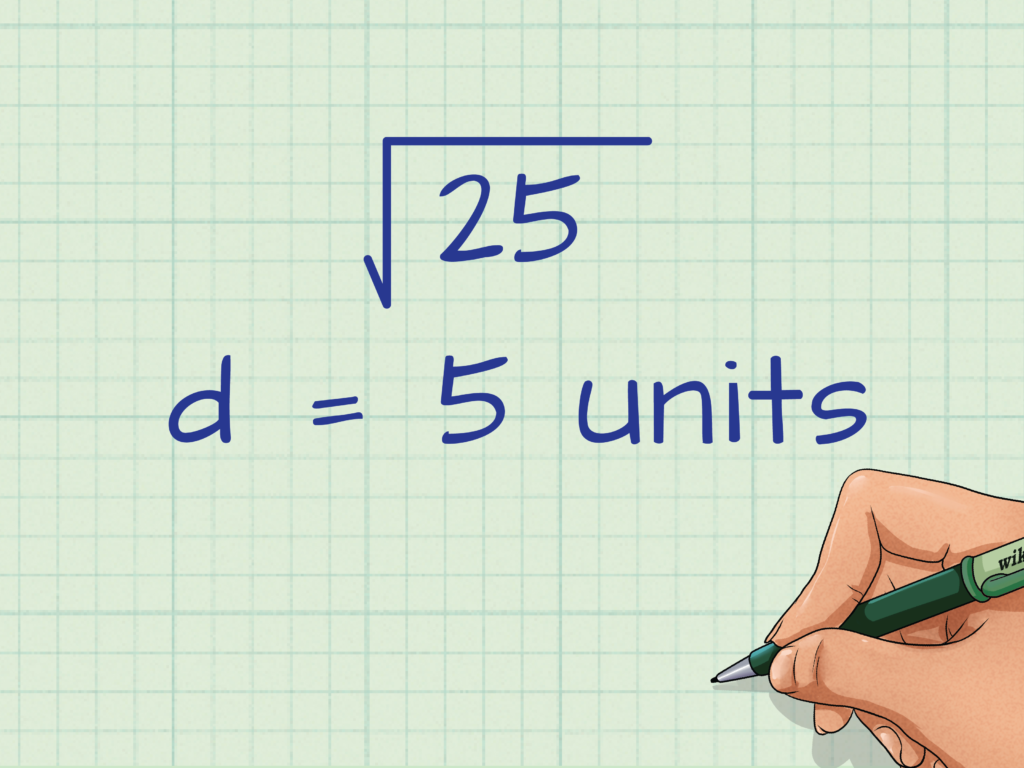
1. Giới Thiệu Về Đoạn Thẳng
1.1. Định Nghĩa Đoạn Thẳng
Đoạn thẳng là phần của đường thẳng nằm giữa hai điểm, bao gồm cả hai điểm đầu mút này. Ví dụ, đoạn thẳng AB là đường thẳng giữa điểm A và điểm B. Đoạn thẳng có thể nằm trên mặt phẳng hoặc trong không gian ba chiều.
1.2. Độ Dài Đoạn Thẳng
Độ dài của đoạn thẳng là khoảng cách giữa hai điểm đầu mút của đoạn thẳng đó. Đơn vị đo có thể là mm, cm, dm, m, km tùy thuộc vào hệ thống đo lường được sử dụng.
2. Công Thức Tính Độ Dài Đoạn Thẳng
2.1. Công Thức Trong Mặt Phẳng
Trong mặt phẳng tọa độ Oxy, độ dài đoạn thẳng AB giữa hai điểm A(x₁, y₁) và B(x₂, y₂) được tính bằng công thức:
AB=(x2−x1)2+(y2−y1)2
2.2. Công Thức Trong Không Gian
Trong không gian ba chiều Oxyz, độ dài đoạn thẳng AB giữa hai điểm A(x₁, y₁, z₁) và B(x₂, y₂, z₂) được tính bằng công thức:
AB=(x2−x1)2+(y2−y1)2+(z2−z1)2
3. Ví Dụ Minh Họa
3.1. Ví Dụ Trong Mặt Phẳng
Giả sử chúng ta có hai điểm A(2, 3) và B(5, 7). Để tính độ dài đoạn thẳng AB, ta áp dụng công thức:
AB=(5−2)2+(7−3)2=32+42=9+16=25=5
Vậy, độ dài đoạn thẳng AB là 5 đơn vị.
3.2. Ví Dụ Trong Không Gian
Giả sử chúng ta có hai điểm A(1, 2, 3) và B(4, 6, 8). Để tính độ dài đoạn thẳng AB, ta áp dụng công thức:
AB=(4−1)2+(6−2)2+(8−3)2=32+42+52=9+16+25=50≈7.07
Vậy, độ dài đoạn thẳng AB là khoảng 7.07 đơn vị.
4. Ứng Dụng Thực Tiễn
4.1. Trong Hình Học
Việc tính toán độ dài đoạn thẳng là cơ sở cho nhiều bài toán hình học khác nhau, từ việc tính chu vi, diện tích của các hình đa giác đến việc xác định khoảng cách giữa các điểm trong không gian.
4.2. Trong Vật Lý
Trong vật lý, công thức tính độ dài đoạn thẳng được sử dụng để tính khoảng cách giữa các điểm trong không gian, từ đó xác định các đại lượng vật lý như vận tốc, gia tốc.
4.3. Trong Kỹ Thuật và Công Nghệ
Trong kỹ thuật và công nghệ, việc tính toán độ dài đoạn thẳng giúp xác định kích thước, khoảng cách giữa các bộ phận của máy móc, thiết bị, đảm bảo tính chính xác và hiệu quả trong thiết kế và sản xuất.
5. Bài Tập Thực Hành
5.1. Bài Tập 1
Cho hai điểm A(3, 4) và B(7, 1). Tính độ dài đoạn thẳng AB.
Giải:
AB=(7−3)2+(1−4)2=42+(−3)2=16+9=25=5
Vậy, độ dài đoạn thẳng AB là 5 đơn vị.
5.2. Bài Tập 2
Cho hai điểm A(-2, -3, 4) và B(1, 2, -1). Tính độ dài đoạn thẳng AB.
Giải:
AB=(1−(−2))2+(2−(−3))2+(−1−4)2=32+52+(−5)2=9+25+25=59≈7.68
Vậy, độ dài đoạn thẳng AB là khoảng 7.68 đơn vị.
6. Kết Luận
Công thức tính độ dài đoạn thẳng là một công cụ quan trọng trong toán học và nhiều lĩnh vực khác. Việc nắm vững công thức này không chỉ giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả mà còn ứng dụng vào nhiều tình huống thực tế trong cuộc sống. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn hiểu rõ hơn về cách tính độ dài đoạn thẳng.
Nếu bạn có bất kỳ câu hỏi hoặc thắc mắc nào, hãy truy cập trang web chính thức của International Mathematical Olympiad tại imo-offial.org để tìm hiểu thêm và nhận được sự hỗ trợ từ các chuyên gia toán học hàng đầu.